poj3009--Curling 2.0(搜索练习1)
Description
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
- At the beginning, the stone stands still at the start square.
- The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
- When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
- Once thrown, the stone keeps moving to the same direction until one of the following occurs:
- The stone hits a block (Fig. 2(b), (c)).
- The stone stops at the square next to the block it hit.
- The block disappears.
- The stone gets out of the board.
- The game ends in failure.
- The stone reaches the goal square.
- The stone stops there and the game ends in success.
- The stone hits a block (Fig. 2(b), (c)).
- You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.
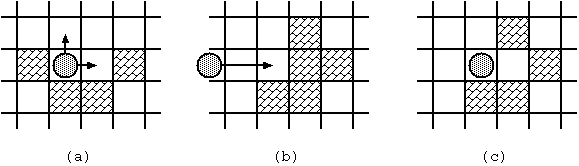
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
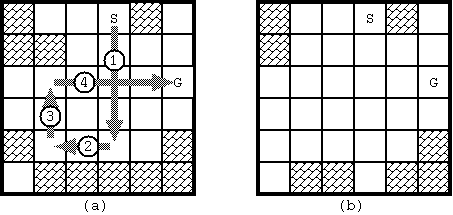
Fig. 3: The solution for Fig. D-1 and the final board configuration
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
Output
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
Sample Input
2 1 3 2 6 6 1 0 0 2 1 0 1 1 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 6 1 1 1 2 1 1 3 6 1 1 0 2 1 1 3 12 1 2 0 1 1 1 1 1 1 1 1 1 3 13 1 2 0 1 1 1 1 1 1 1 1 1 1 3 0 0
Sample Output
1 4 -1 4 10 -1
题目大意:冰壶游戏,从起点开始,每次移动都要撞到石头或经过终点才会停止,如果碰到边界就会毁坏,在撞到石头后,停在石头的前一个位置,石头被撞碎,以后就可以经过那个点了。当冰壶紧挨着石头的时候,冰壶不能撞碎石头(如果步数大于10,输出-1)
因为在不断的运动中,图是在变化的,所以只能用dfs的做法,从起点开始,深搜,每次判断上下左右能不能走
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;
struct node{
int x , y , step ;
};
int Map[25][25] , step , n , m , s , e ;
void dfs(node p)
{
if( p.step > 10 || ( p.x == s && p.y == e ) )
{
step = min(step,p.step) ;
return ;
}
int i , j ;
node q ;
if( (!Map[p.x-1][p.y] || (p.x-1 == s && p.y == e) ) )
{
for(i = p.x-1 ; i >= 0 ; i--)
if( Map[i][p.y] == 1 )
break ;
if( i > 0 )
{
q = p ;
if( i == s && p.y == e )
q.x = i ;
else
q.x = i+1 ;
q.step++ ;
Map[i][p.y] = 0 ;
dfs(q) ;
Map[i][p.y] = 1 ;
}
}
if( ( !Map[p.x+1][p.y] || (p.x+1 == s && p.y == e) ) )
{
for(i = p.x+1 ; i <= n+1 ; i++)
if( Map[i][p.y] == 1 )
break ;
if( i < n+1 )
{
q = p ;
if( i == s && p.y == e )
q.x = i ;
else
q.x = i-1 ;
q.step++ ;
Map[i][p.y] = 0 ;
dfs(q) ;
Map[i][p.y] = 1 ;
}
}
if( (!Map[p.x][p.y-1] || (p.x == s && p.y-1 == e) ) )
{
for(j = p.y-1 ; j >= 0 ; j--)
if( Map[p.x][j] == 1 )
break ;
if( j > 0 )
{
q = p ;
if( q.x == s && j == e )
q.y = j ;
else
q.y = j+1 ;
q.step++ ;
Map[q.x][j] = 0 ;
dfs(q) ;
Map[q.x][j] = 1 ;
}
}
if( (!Map[p.x][p.y+1] || (p.x == s && p.y+1 == e) ) )
{
for(j = p.y+1 ; j <= m+1 ; j++)
if( Map[p.x][j] == 1 )
break ;
if( j < m+1 )
{
q = p ;
if( q.x == s && j == e )
q.y = j ;
else
q.y = j-1 ;
q.step++ ;
Map[q.x][j] = 0 ;
dfs(q) ;
Map[q.x][j] = 1 ;
}
}
return ;
}
int main()
{
int i , j ;
node p ;
while( scanf("%d %d", &m, &n) && ( m || n ) )
{
step = 11 ;
memset(Map,0,sizeof(Map)) ;
for(i = 1 ; i <= n ; i++)
for(j = 1 ; j <= m ; j++)
{
scanf("%d", &Map[i][j]) ;
if( Map[i][j] == 2 )
{
p.x = i ; p.y = j ; p.step = 0 ;
Map[i][j] = 0 ;
}
if( Map[i][j] == 3 )
{
s = i ; e = j ;
Map[i][j] = 1 ;
}
}
dfs(p) ;
if( step > 10 )
step = -1 ;
printf("%d\n", step) ;
}
return 0;
}
郑重声明:本站内容如果来自互联网及其他传播媒体,其版权均属原媒体及文章作者所有。转载目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,也不构成任何其他建议。




































