题目链接:

思路是：首先根据图像抽象出联通关系。。首先确定每一种图形的联通关系，用01值表示不连通与不连通。。。然后从第1个图形进行dfs搜索。如果碰到两快田地可以联通的话那么标记。。注意处理的过程中你的

搜索顺序要和你的每个图形的连通性的顺序相同。。然后就是最后看上下。左右能否匹配。。。看最后有几个不同的快，这就是答案，感觉跟并查集一样。。并查集应该也可以做。。

题目：

Farm Irrigation

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5696    Accepted Submission(s): 2474

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.


Figure 1

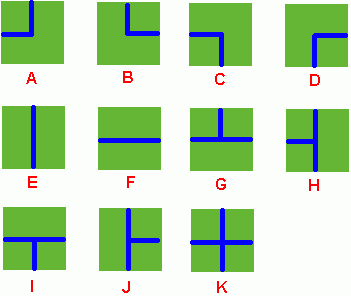
Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map 

ADC
FJK
IHE

then the water pipes are distributed like 


Figure 2

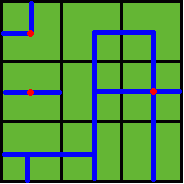
Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. 

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him? 

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of ‘A‘ to ‘K‘, denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2
DK
HF

3 3
ADC
FJK
IHE

-1 -1

 

Sample Output

2
3

 

Author

ZHENG, Lu

 

Source

Zhejiang University Local Contest 2005

 

Recommend

Ignatius.L   |   We have carefully selected several similar problems for you:  1232 1213 1856 1811 1829 

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;

int n,m,ans;
const int maxn=50+10;
int map[maxn][maxn];

int dX[]={-1,0,1,0};
int dY[]={0,1,0,-1};

int pipe[11][4]={{1,0,0,1},{1,1,0,0},{0,0,1,1},{0,1,1,0},{1,0,1,0},{0,1,0,1},{1,1,0,1},{1,0,1,1},{0,1,1,1},{1,1,1,0},{1,1,1,1}};
int hash[maxn][maxn];

bool check(int row,int col)
{
    if(row>=0&&row<n&&col>=0&&col<m&&!hash[row][col])
        return true;
    return false;
}

void dfs(int row,int col)
{
    hash[row][col]=1;
    for(int k=0;k<4;k++)
    {
        int dx=row+dX[k];
        int dy=col+dY[k];
        if(check(dx,dy)&&pipe[map[row][col]][k]==1&&pipe[map[dx][dy]][(k+2)%4]==1)
           dfs(dx,dy);
    }
}

void solve()
{
    memset(hash,0,sizeof(hash));
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
    {
       if(!hash[i][j])
        {
           dfs(i,j);
            ans++;
        }
    }
}

int main()
{
    char str[maxn];
    while(~scanf("%d%d",&n,&m))
    {
        ans=0;
        if(n<=0||m<=0)  return 0;
        for(int i=0;i<n;i++)
        {
            scanf("%s",str);
            for(int j=0;j<m;j++)
                map[i][j]=str[j]-'A';
        }
        solve();
        printf("%d\n",ans);
    }
    return 0;
}

hdu1198Farm Irrigation(dfs找联通),,5-wow.com