The Willy Memorial Program （poj 1073 ,联通水管注水模拟）

浏览数：92 / 时间：2015年06月11日

Description

Willy the spider used to live in the chemistry laboratory of Dr. Petro. He used to wander about the lab pipes and sometimes inside empty ones. One night while he was in a pipe, he fell asleep. The next morning, Dr. Petro came to the lab. He didn‘t notice Willy while opening the valve to fill the pipes with hot water. Meanwhile, Stanley the gray mouse got what was going to happen. No time to lose! Stan ran hard to reach the valve before Willy gets drawn, but... Alas! He couldn‘t make it!

Poor Willy was boiled in hot water, but his memory is still in our hearts. Though Stan tried his best, we want to write a program, in the memory of Willy, to compute the time Stan had, to rescue Willy, assuming he started to run just when the doctor opened the valve.

To simplify the problem, assume the pipes are all vertical cylinders with diameter 1 cm. Every pipe is open from the top and closed at the bottom. Some of the pipes are connected through special horizontal pipes named links. The links have very high flow capacity, but are so tiny that at any given time, the volume of water inside them is negligible. The water enters from top of one of the pipes with a constant rate of 0.25PI cm³/sec and begins to fill the pipe from the bottom until the water reaches a link through which it flows horizontally and begins to fill the connected pipe. From elementary physics we know if two pipes are connected and the surface of the water is above the connecting link, the level of water in both pipes remains the same when we try to fill one of them. In this case the water fills each pipe with a rate equal to half of the rate of incoming water. As an example, consider the following configuration:

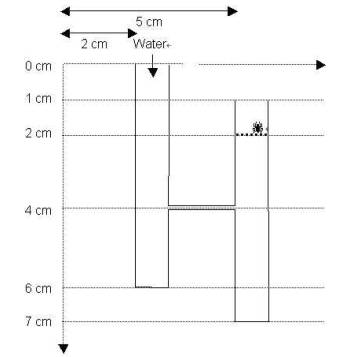
First, the lower 2 centimeters of the left pipe is filled with water at full rate, then, the lower 3 centimeters of the right pipe is filled, and after that, the upper part of the two pipes are filled in parallel at half rate. The input to your program is a configuration of pipes and links, and a target level in one of the pipes (the heavy dotted line in the above figure). The program should report how long it takes for the level of water to reach the target level. For the above configuration, the output is 9 seconds.

It is assumed that the water falls very rapidly, such that the time required for the water to fall can be neglected. The target level is always assumed to be a bit higher than the specified level for it. As an example, if we set the target point to level 4 in the left pipe in the figure above, the elapsed time for water to reach that target is assumed to be 5 (not 2), Also note that if the water reaches to the top of a pipe (say in level x), it won‘t pour out outside the pipe until empty spaces in connected pipes below level x are filled (if can be filled, i.e. the level of water reaches the connecting links). (Note that there may be some links at level x, to which water is entered). After all such spaces are filled; the water level would not go up further.

Input

To describe positions, we assume the coordinates are expressed as (x, y) and the origin lies in the top-left of all pipes and links. (Note that y coordinates are increased downwards). All coordinates are integer numbers between 0 and 100, inclusive.
The first line of the input file contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. The first line of each test case is p (1 <= p <= 20), the number of pipes, followed by p lines, each describing a pipe. Each pipe description line consists of three numbers. The first two are (x, y) coordinates of the upper-left corner of the pipe and the third number is the height of the pipe (at least 1 cm and at most 20 cm). Note that diameter of each pipe is 1 cm.

After input data describing the pipes, there is a line containing a single integer l, which is the number of links (0 <= l <= 50). After it, there are l lines describing links. Each link description contains 3 integers. The first two are (x, y) coordinates of the left end-point of the link and the third is the length of the link (at least 1 cm and at most 20 cm). It is assumed that the width of the link is zero.

The last line for each test case contains two numbers. The first is the number of target pipe (starting from one, with the order appeared in test data). The second line is the desired y for the level of water in the target pipe (note that the specified level may be out of the pipe at all).

You can assume the following about the input:
. The water enters into the first pipe.
. No link crosses a pipe.
. No two links have the same y coordinates.
. No two pipes have the same upper-left x coordinates.
. Both endpoints of each link are connected to pipes.

Output

The output should contain exactly t lines with no blank lines in between, each corresponding to one test case. Each output line should contain the time required for the water to reach the target level in the target pipe (an integer number). If in a specific test case, the water never reaches the target level, the line should contain No Solution string in it.

Sample Input

Sample Output

Source

Tehran 2001

题目大意：有一些竖直的圆筒状管子，管子间有理想的水平细管相连。一只蜘蛛停在某跟管子的某个高度上，从第一根管子往系统注水，问前往营救的蜘蛛有多长时间可以关闭热水阀门。最终抽象为当水上升到指定位置的时候系统中的总水柱高度。这里第一行数据表示有t种情况,接下来2表示有2个管子，第三行和第四行分别表示这2个管子的左上角坐标和管子的长度，下面的1表示有1个连接，该链接左端坐标（3,4），长为2，接下来的2,2表示蜘蛛在第2号管子的y=2处。

解题思路：从第一根管子开始注水，采用优先队列的方式每次选取可注水且纵坐标最大（最低）的地方进行注水。若中途出现溢出现象(从其他管子的上端流出），则永远都淹不到蜘蛛。

相关知识：pair 的用法 http://www.cnblogs.com/Nimeux/archive/2010/10/05/1844191.html

lower_bound的用法 http://blog.csdn.net/niushuai666/article/details/6734403

  1 #include <iostream>
  2 #include <cstring>
  3 #include <string>
  4 #include <string.h>
  5 #include <set>
  6 #include <list>
  7 #include <queue>
  8 using namespace std;
  9 #define maxp 30
 10 
 11 int cases,pipes,links,target,level,tot_water;
 12 int w,p,pp;
 13 int px[maxp],py[maxp],bottom[maxp],water[maxp];//一个管道内x,上面y,下面y,当前水位
 14 bool find_ans;
 15 set<int> link;//保存连接的y值
 16 list<pair<int, int> > e[maxp];//保存管i上的连接的位置和另一端的管的编号
 17 priority_queue<pair<int, int> > pq;//保存当前水位(y值和管道标号)
 18 
 19 void read(){
 20     cin>>pipes;//输入管道
 21     for(int i=0;i<pipes;i++){
 22         int tmp;
 23         cin>>px[i]>>py[i]>>tmp;
 24         bottom[i]=py[i]+tmp;    //管i的底部y值
 25         water[i]=-1;            //标记means !visit pipe i
 26         e[i].clear();
 27     }
 28     cin>>links;//输入连接
 29     link.clear();
 30     for(int i=0;i<links;i++){
 31         int lx,ly,len,lk1=-1,lk2=-1;
 32         cin>>lx>>ly>>len;//输入每个连接并计算该连接连的管道lk1,lk2
 33         for(int j=0;j<pipes;j++){
 34             if(bottom[j]>=ly && py[j]<=ly){
 35                 if(px[j]+1==lx)lk1=j;
 36                 if(px[j]==lx+len)lk2=j;
 37                 if(lk1!=-1 && lk2!=-1)break;
 38             }
 39         }
 40         link.insert(ly);
 41         e[lk1].push_back(make_pair(ly, lk2));
 42         e[lk2].push_back(make_pair(ly, lk1));
 43     }
 44     cin>>target>>level;
 45     link.insert(level);//把蜘蛛的位置也传入连接!!!
 46     target--;
 47 }
 48 bool init(){
 49     if(level<py[target]){
 50         cout<<"No Solution\n";
 51         return 0;
 52     }//当蜘蛛在管道外时,无解
 53     //如果蜘蛛位于target管道中就虚拟一个target和-2管相连的连接(-2可以起到标记作用)
 54     if(py[target]<=level && level<=bottom[target])
 55         e[target].push_back(make_pair(level,-2));
 56     //延长每条连接把与每个管道的交点保存成i和i管相连的连接的形式
 57     //把每个管道的上端标记为其和-1相连的形式，并把e[i]排序颠倒
 58     for(int i=0;i<pipes;i++){
 59         for(set<int>::const_iterator j=link.lower_bound(py[i]);
 60             j!=link.end()&&*j<bottom[i];j++){
 61             e[i].push_back(make_pair(*j,i));
 62         }
 63         e[i].push_back(make_pair(py[i],-1));
 64         e[i].sort();
 65         e[i].reverse();
 66     }
 67     return 1;
 68 }
 69 void solve(){
 70     while (!pq.empty())pq.pop();//清空pq
 71     water[0]=bottom[0];
 72     pq.push(make_pair(water[0],0));//从第一个管道开始倒水
 73     find_ans=false;
 74     tot_water=0;
 75     while (!pq.empty()){
 76         w=pq.top().first;   //water   
 77         p=pq.top().second;  //pipe
 78         pq.pop();
 79         if(p==-1)break;//溢出
 80         else if(p==-2){//淹没
 81             find_ans=true;
 82             break;
 83         }
 84         tot_water+=(water[p]-w);//把p管流到w位置
 85         water[p]=w;
 86         //把当前w位置所有与p连接的处理
 87         while(!e[p].empty() && e[p].front().first==water[p]){
 88             pp=e[p].front().second;
 89             if(pp<0)pq.push(e[p].front());//如果不是实连接(-1,-2的情况)直接放入pq中
 90             else if(water[pp]==-1){//如果实连接且还没有水，就更新该管水位，并放入pq中
 91                 water[pp]=bottom[pp];
 92                 pq.push(make_pair(water[pp], pp));
 93             }
 94             e[p].pop_front();
 95         }
 96         if(!e[p].empty()) pq.push(make_pair(e[p].front().first, p));//如果p管还有连接，就把它放入pq中
 97     }
 98 }
 99 int main(){ 
100     cin>>cases;
101     while (cases--){
102         read();
103         if(!init())continue;        
104         solve();
105         if (find_ans)
106             cout<<tot_water<<‘\n‘;
107         else
108             cout<<"No Solution\n";
109     }
110     return 0;
111 }
112         
113