对于enigma machine的破解

浏览数：45 / 时间：2015年06月20日

最近看到一篇文章，详细讲解了二战时期德军的enigma machine是怎样被破解的。enigma machine本质上是利用substitution cipher的原理来进行加密的。

1）替换加密的原理及破解方法

在古代，当人们想要对一段文字进行加密时，会把原文（即明文）中的字母按照某种配对关系替换成其他的字母，从而得到一段别人看不懂的密文。

例如我们可以按照以下的配对关系对明文进行加密：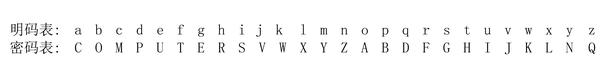

在加密过程中，第一行明码表中的字母分别被替换成位于该字母下方的大写字母。加密结束后，将会得到一段不经解密谁也看不懂的密文。

比方说我们现在要对下面这段明文进行加密：

when you are old and grey and full of sleep

按照上面的替换规则加密后，我们将得到一段密文：

KRUZ NAI CFU AXP CZP EFUN CZP TIXX AT GXUUB

就这样，我们完成了一次替换加密。我们得到的这段密文被破解的难度有多大呢？理论上讲，破解者可以用各种可能的密码表组合来试着解密这段话。但由于26个字母可能的排列顺序有4.03X10^26种之多，这意味着如果全世界60亿人每人每秒可以测试一种可能的密码表，也需要21亿年才能试完所有的排列组合。事实上，在很长的一段时间里，这种简单的替换密码被认为是无法被破解的。

按理说，我们的故事到这里就应该结束了。靠着这种无法被破解的密码，密码的发送者和接收者像童话里的王子和公主一样，从此过上了永远幸福的生活。

但是，在这个世界上，偏偏就是有人能想出巧妙的方法来破解这种看似无懈可击的密码。他们所使用的武器是语言学和统计学。

在使用字母文字的语言中，每一个字母在普通的文本中出现的概率事实上是不同的。以英语为例，在一篇普通的文章中，字母e, a, t出现的概率远远大于j, x, z出现的概率。如果对足够多的文本进行分析，我们就可以统计出每一个字母在英语文本中出现的平均概率。

下面这张图片来自维基百科，显示的是26个字母在普通的英文文本中出现的概率：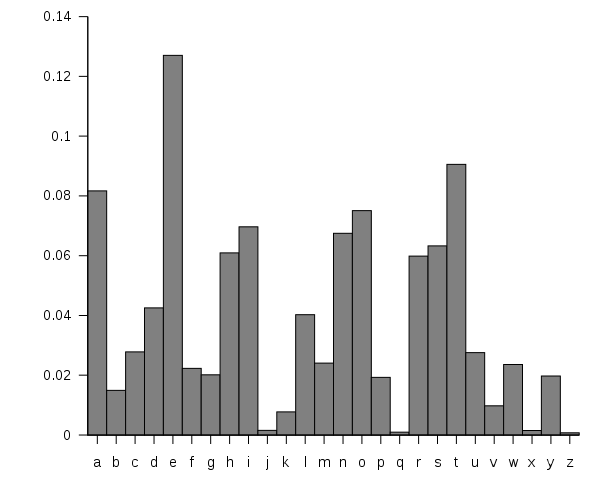

我们刚刚进行的替换加密中，虽然每一个字母都改头换面变成了另一个字母，但这并不能改变它在一段文本中出现的频率。例如在刚刚的加密过程中，字母e被替换成了U，如果我们截取足够长的密文进行分析的话，我们会发现在密文中字母U出现的频率要远远高于其他字母。只要对照上面这张概率图，把密文中出现频率最高的几个字母依次试着替换为e, t, a这几个高频字母，就可以对密文进行破解。

作为辅助手段，我们还可以统计密文中每个字母左右两边的字母出现频率。如果一个字母可以出现在大多数字母的两旁，那么它很有可能是一个元音字母。反之，如果一个字母永远也不会出现在某些特定字母的旁边，那么它很可能是一个辅音字母，因为在英语中一些辅音字母是永远不会被拼写在一起的。

至此，我们上面介绍的这种单字母替换密码被无情的破解了。

于是，不死心的密码师们又发明了多字母替换密码。

上面这张表叫做维热纳尔方阵（Vigenère square），是为了方便加密者进行多字母替换而设计的。人们可以在表中选取任意行数的字母作为密码表进行加密，进一步提高了密码的复杂程度。

然而，“每加密一个字母就更换一次密码表并且永不重复”的替换密码已经超出了人力所及的范围。

不过，人类做不到的事情，不代表机器也无法做到。

接下来，让我们来看一下恩格玛机的工作原理。

2）恩格玛机的工作原理

请自行google

3）恩格玛机的破解

在军用恩格玛机投入使用之后，英法情报机构曾经试着将其破译，结果发现自己就像《格雷的五十度灰》里的女主角一样被虐了个死去活来。经过多次尝试之后，他们宣布这种密码系统是无解的。

如果有人正期待着图灵在这一部分的开头闪亮登场，我不得不遗憾地告诉你，破解恩格玛机的第一次突破并不是来自英国人，而是波兰人雷耶夫斯基（Marian Rejewski）。

再来总结一下我们第二部分中讲过的内容，想要破译一份被恩格玛机加密的密文，波兰人需要以下三部分信息：

a）恩格玛机的工作原理及内部构造，包括每个转子的线路连接；
b）德军的对恩格玛机的操作守则；
c）德军所使用的每日初始设置。恩格玛机的每日初始设置包含了三个信息：即转子的排列顺序、每个转子的初始位置、以及插线板的设置。这些信息被印刷在密码本上分发至全军，每24小时更换一次设置，每月更换一次密码本；

长话短说，通过间谍活动以及出色的数学能力，波兰人得到了a）和b）这两部分信息。

接下来，波兰人需要做的就是破解德军所使用的每日初始设置（下文简称为日密钥）。

我们再来回顾一下德国操作员是如何进行一次加密的：

首先，操作员会根据日密钥对恩格玛机进行初始设置。例如他会将三个转子的排列顺序按照日密钥的指示排列为2-3-1，然后将三个转子的顺序依次旋转到Q-V-M的位置，最后在插线板上将六对字母进行互换。

再发送每一条信息前，操作员都会任意挑选三个此刻在自己脑子中冒出的字母，比如说XYZ，作为本条信息的密钥，下文称之为信息密钥。

操作员在发送信息前，会先使用日密钥中的设置，也就是转子处在Q-V-M的位置，将XYZ输入两次，得到比如说HGABLE。注意这里随着转子的转动，两次输入的XYZ被加密成了不同的字母。接着，操作员将恩格玛机的三个转子重新转到X-Y-Z的位置，然后将信息的正文输入恩格玛机后发送。

处在接收方的操作员，同样是按照日密钥将恩格玛机设置好，然后将信息开始的6个字母HGABLE输入恩格玛机，得到XYZXYZ，那么他就是知道XYZ是加密正文所使用的信息密钥。接下来，他只需将三个转子的位置转到X-Y-Z，然后将剩下的部分输入就会得到信息的正文。

这种操作方法的奥秘之处在于，每一条信息的正文都是用不同的密钥进行加密的，从而大大避免了被破解的可能性。只有每条信息的前六个字母是以通用的日密钥加密的。这看起来是一个完美的解决方案，但是雷耶夫斯基用令人难以置信的洞察力，发现了其中的一个漏洞。

我们想象雷耶夫斯基截取到了一段德军的电文，前六个字母是HGABLE。他知道这是三个字母连续输入两次恩格玛机后得到的结果。虽然我们不知道这三个字母是什么，但我们知道输出结果HGABLE中第一个字母H和第四个字母B是同一个字母的加密结果。由于转子在期间转动了三次，所以同一个字母在两次加密时被替换成了不同的字母。我们可以把它们组成一对：

H - B

如果雷耶夫斯基在一天之内截获到了更多的电报，对每封电报的前六个字母进行类似的操作，就会得到更多的字母对，直至26个字母都配上对：

H - B
A - O
……
Z - U

这看起来只是一个无聊的字母配对游戏而已，跟破解恩格玛机一点关系也没有。但是，雷耶夫斯基凭借非凡的洞察力，利用每条信息前这区区六个字母，找到了破解之道。

答主看到很多人在评论区里很淡定的表示这篇文章一点都不烧脑。答主在这里想说，嗯，那是因为本文真正烧脑的内容根本还没开始呀……

在阐述雷耶夫斯基的思路之前，我需要大家认真地思考一个问题：

恩格玛机的本质究竟是什么？

你在恩格玛机上敲入一个字母，它会输出另外一个字母。这就是恩格玛机的本质：字母替换。

在一个相同的设置下，你敲入26个字母中随便哪一个字母，所得到的替换字母都是确定不变的。我们可以将这个替换关系用函数（A0）来表示。你也许会说，恩格玛机是很复杂的，每敲下一个字母后，转子会转动一位，然后就是一种完全不同的替换关系。没关系啊，我们可以把转动一位之后的替换关系用（A1）来表示。类似的，我们用（A2）来表示转子转动两位之后的替换关系用，一直到（A5）表示转子转动五位之后的。

答主在本文中已经最大限度的避免使用数学符号和公示，但在雷耶夫斯基的思路过于抽象，借助一些函数符号反而有助于理解。当你充分理解上一段话的意思之后，让我们再来看一下波兰人截获的六位字母HGABLE。波兰人并不知道这是哪三个字母被加密两次的结果，不过没关系，我们暂且假设它为XYZ。这样，我们可以利用上面的替换关系将加密过程表示为：

X(A0)=H
Y(A1)=G
Z(A2)=A
X(A3)=B
Y(A4)=L
Z(A5)=E

还记得在本文的第二部分，我们提到的恩格玛机的两个非常非常重要的性质吗？其中第一条是恩格玛机是自反的。就是说，如果输入字母A得到字母G，同样的配置下输入字母G就会得到字母A，这同时也是恩格玛机解密的原理。如果用刚才的函数来表示的话就是，一个字母被函数（An）连续替换两次会得到自身，比如：

X(A0)(A0)=X

嗯，好像开始有点意思了，如果我们把前面第四行式子X(A3)=B中的X写成上面这种形式的话，会得到：

X(A0)(A0)(A3)=B

然后从第一行我们已经知道X(A0)=H，所以：

H(A0)(A3)=B

神奇的事情发生了，X这个字母被抵消掉了！也就是说，雷耶夫斯基发现的H和B之间的这种联系与用来加密每一条信息的信息密钥是无关的。这种联系只与恩格玛机在这一天的初始配置相关。在这里，雷耶夫斯基不知道(A0)是什么，也不知道(A3)是什么，但通过前面的字母配对游戏中其他的24 个字母之间的替换关系，雷耶夫斯基可以推导出(A0)(A3)。这个(A0)(A3)所代表的正是是雷耶夫斯基前面所做的那个字母配对游戏中，横线左边的字母被替换成右边的这样一种替换关系。

(A0)(A3)的物理意义就是将一个字母通过恩格玛机的初始设置进行替换后，再将转子向后转动三位将所得的结果再进行一次替换。如果忽略掉中间步骤，从本质上讲它还是一种替换，与本文开头所介绍的最简单的单字母替换密码没有区别，一样可以被写成下面这种形式：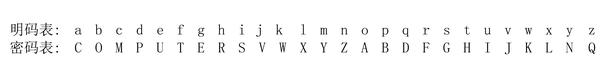

如果我们已经知道了(A0)(A3)所代表的的就是上图这样的替换关系，可以用这个结果对恩格玛机进行暴力破解吗？如果没有插线板的话，这种做法理论上讲是可行的。对于处于任意状态的恩格玛机，我们可以测试每一个字母经过“初始位置”和“旋转三位后位置”两次加密后是否得到了正确的结果。三个转子的排列和初始位置一共有大约十万种可能性，如果制造100台恩格玛机，由100个人同时进行暴力破解，每人10秒钟完成一次检查的话，可以在三个小时内完成暴力破解。

但是由于插线板的存在，将可能的组合数量一下子增加了1000亿倍，彻底地杜绝了一切暴力破解的可能性。在这个时候，雷耶夫斯基又找到了一个方法，巧妙地消除了插线板的影响。

我们来做一个小练习，假设有一个替换密码表，我们一般会把它写成下面的形式（为了方便演示，我这里使用一个只有八个字母的密码）：

明文 A B C D E F G H
密文 C H E F A B D G

我们可以做一个首尾接龙的游戏。比如上表中明文A被替换成密文C，那么我们在第一行中再找到C，发现C被替换成了E，那么在第一行中找到E，发现E被替换回了A，这样我们就完成了一个字母链条。然后我们换一个在上一个链条中没出现过的字母重新开始，直到所有的字母都被列入一个链条。我们将处于同一个链条中的字母写入一个括号内，这个密码表就变成：

(A, C, E) (B, H, G, D, F)

与原先的形式相比，写成这种形式的密码表传递了完全相同的信息。你一样可以知道A应该被替换成C，C应该被替换成E，E应该被替换成A……等等。那么写成这种形式有什么好处呢？这种形式可以揭示一个密码表的一个内在特征，比如上面这个密码表是由两条字母链条组成的，链条长度分别为“3”和“5”。这个“3”和“5”就是这个密码表的特征值。

如果将我们之前得到的(A0)(A3)也改写成这种链条形式的话，会得到这样的结果：

(A, C, M, Y, N, Z, Q, D, P, B, O) (E, U, I, S, G) (F, T, H, R) (J, V) (K, W) (L, X)

可见，这个(A0)(A3)所对应的密码表一共由6个字母链条组成，长度分别是“11”、“5”、“4”、“2”、“2”、“2”。

插线板可以将恩格玛机设置的组合数量提高1000亿倍，也可以将密码表中的字母替换地面目全非。但由于插线板是将字母成对地进行交换，这种交换方式不会改变密码表的链条数量及长度。在上面写成链条形式的密码表中，任意交换两个字母的位置，无论交换多少次也不会改变链条的数量和长度。

就这样，雷耶夫斯基成功地找到了绕开插线板的方法。

对应恩格玛机转子设置十万种可能的组合，波兰人对每一种组合所产生的字母链条数量和长度进行了分类（说起来容易，这花了一年的时间）。有了这样一个分类目录，波兰人就可以按照以下步骤进行破解：

a) 首先根据当日截获的每一封电报的前六个字母推导出字母链条的数量和长度
b) 接着在分类目录里找到相应的可能转子设置（一个比十万小得多的数量）
c) 针对所有可能的转子设置进行暴力破解。

到这里，波兰人已经拿到了德军日密钥中除了插线板设置以外所有的内容。

得到转子的设置之后，雷耶夫斯基将会把一台恩格玛机按照这种设置装好，但是插线板完全不插任何电线，然后把一段密文输入这台机子。他会得到一段没有意义的信息，因为信息中的六对字母被随机对调了。但是这种字母互换只是一种非常初级的加密方式，可以使用人工轻松地破解。这样，破解者又拿到了插线板设置。

这样，波兰人拿到了德军日密钥中的全部内容。也就是说，雷耶夫斯基与德军中的接收员处在了完全对等的地位，德军所有的通讯对于波兰人来说都是完全透明的——至少在当天午夜十二点之前是这样。

如果恩格玛机就这样被波兰人破解了，那还关图灵什么事呢？

德军在二战爆发前后，又采取了很多措施来加强恩格玛机的安全性（变态啊），其中的一些使得波兰人上面的这种破解方法失效：

a) 1938年9月15日开始，德军干脆连日密钥中的转子位置也让操作员自己选择。这样一来，就连每条信息的前六个字母也变成是用不同密钥加密的了。
b) 1938年12月15日，德军把转子的数量从三个增加到了五个，安装的时候从五个里面随机选三个安装在恩格玛机上，将可能的转子组合增加了10倍。更重要的是，有了多出来的转子，波兰人做的分类目录就失效了。
c) 1939年1月1日，德军把插线板上交换字母的最大数量从6对增加到了10对。
d) 1940年5月1日，德军规定每条信息的信息密钥发送一遍即可，无需重复两次。

接下来，该英国人出场了。

================补充说明开始的分割线==============

在图灵正式出场之前，由于评论里有好几个人表示上面德军新操作守则里的a)看不懂，答主在这里再简单说明一下。

在后期的恩格玛机中，德军又对转子进行了改造，使得转子芯外面的字母圈可以绕着转子旋转。这样一来，德军的日密钥内容就变成了以下三个部分：

1) 从五个转子中选择三个特定的转子，并按一定顺序排列；
2) 每个转子外侧的字母圈相对于转子芯的位置；
3) 插线板所交换的10对字母；

这里请大家注意，在德军实行新规定之后，日密钥中已经不存在每日通用的转子初始位置。在发送每一条信息前，操作员都要自己选择转子初始位置，然后再自己选择本条信息的信息密钥。

举例来说，操作员按照密码本上的日期对恩格玛机完成三项设置后，准备发送一条信息。在发送前，他选择了ABC和XYZ分别作为转子初始位置和信息密钥。他首先把恩格玛机的三个转子拨动到A-B-C的位置上，键入两次XYZ后得到HBLZQO，这样就完成了对信息密钥的加密。接着他把恩格玛机的转子拨动到X-Y-Z的位置上继续输入信息的正文。

评论区很多人的问题是那么这个操作员怎样把ABC这个转子初始位置发送给接收方呢？答案是用明文发送。是的，你没看错，就是明文发送！所以操作员将会依次以明文发送ABC，接着是加密过的HBLZQO，最后是以信息密钥加密后的信息正文。

接收方收到以上信息后，会首先将恩格玛机拨动到ABC的位置，键入HBLZQO后得到XYZXYZ，于是他知道接下来的信息正文是用密钥XYZ加密的。接着他只要把恩格玛机转动到XYZ的位置键入密文，就可以得到信息的明文。

就算破解者截获到这段电报并且知道ABC是明文，也无法知道本条信息的信息密钥。因为破解者不知道德国人手中恩格玛机上的字母圈相对于转子被旋转了多少位，所以并不知道ABC所对应的转子真实位置到底是什么。

雷耶夫斯基巧妙的利用了德军“每条信息的前六个字母都是用同一个通用密钥加密”这一点来进行破解。但是德军采取上述做法之后，每条信息前面的这六位字母都变成是用不同的密钥加密的。所以雷耶夫斯基的破解方法也随之失效。

不过，这个时候的波兰人又想出了另外一种有效的方法进行破解（人类智力的潜能真是无穷无尽啊），直到1940年德国人规定信息密钥只需输入一次后，才彻底失效。考虑到本文的篇幅，这里就不做介绍了。

================补充说明结束的分割线==============

在1939年德军入侵波兰前夕，波兰人将恩格玛机的复制品以及他们所掌握的破解方法提供给了英法两国。波兰人向英国人证明了恩格玛并不是一种完美无缺的密码系统，并且表明了数学知识在破解中的重要性。

不知道英国人在得知波兰人的工作成果之后是怎样的心情，也许震惊之余还会夹杂着一点点惭愧吧。这可是曾经培育出牛顿的国度，在之前竟然如此轻易就放弃了尝试。

波兰人对于英国人士气的激励更多的是在心理层面而不是在技术层面。图灵虽然赞叹波兰人的智慧，但也清醒地认识到波兰人的破解方法过于依赖德国人操作方式上的漏洞。一旦德国人停止将信息密钥重复输入两次，这种破解方法将在一夜之间彻底失效。图灵所追求的破解方式是一种更加纯粹、更加直接的暴力破解。

如果说波兰人是利用敌人防线上的漏洞进行伞兵奇袭，那么图灵想要的更像是步兵师的正面对抗。机器创造出来的密码怪兽，只有用机器才能战胜。而人类的任务不过是设计机器的工作原理以及优化机器所要进行的运算量。

做了这么长的铺垫，终于要进入大结局了。我们来一起看一下英国人的破解恩格玛机的。

首先，英国人需要在密文中确定一条“Crib”。所谓Crib，指的是一段猜测出来的明文与密文中字母的一一对应关系。在密文中猜测出几个单词的明文并不困难，因为循规蹈矩的德国人在信息正文中喜欢用固定的词组，比如Keine besonderen Ereignisse（无特殊情况），Heil Hitler（希特勒万岁）等。另外一个例子是英国人发现德国人喜欢在早上6点钟发送一条天气预报，所以在早上6点钟截获的电文开头中肯定包含 wetter（天气）这个词。

猜出密文中包含的明文单词后，如何精确地确定它们的位置呢？希望你还没有忘记我们前面讲过的恩格玛机的第二个非常非常重要的性质，那就是一个字母永远不会被替换为自身。根据恩格玛机的这个特性，我们可以把一段明文字母在猜测对应的密文上方来回移动进行判断。下面我们用德文单词wetter做一个简单的示例：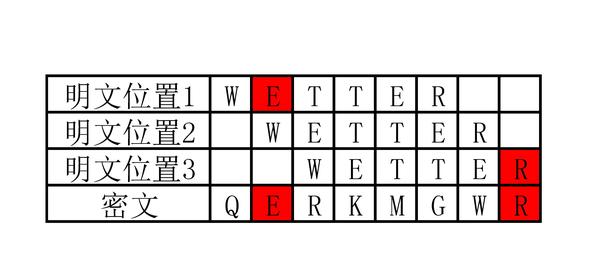

在上面这张图片中，明文位置1可以被排除掉，因为在这个位置上明文中的E又被加密成了E，而这是违反恩格玛机特性的。同理，明文位置3也可以被排除掉，因为明文中的R又被加密成了R。排除掉不可能的情况，明文位置2就极有可能是wetter这个单词所处的真实位置。这样我们就得到了一个Crib，其中明文与密文的对应关系如下：

明文 W E T T E R
密文 E R K M G W

在上面的对应关系中，图灵利用其中首尾相接的字母链，设计出了可以暴力破解恩格玛机的机器。在这段Crib中，明文中的W被加密成E，转子转动一位后E被加密成R，转子转动五位之后R又被加密成W。我们可以把它们之间的关系表示成下面的样子：

W -> 转子位置0加密 -> E -> 转子位置1加密 -> R -> 转子位置5加密 -> W

我们来详细观察一下恩格玛机将字母W加密成字母E这个过程：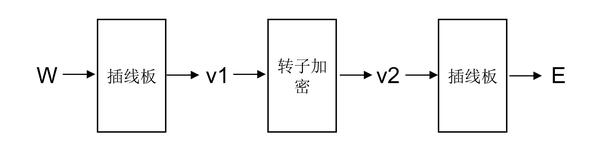

当操作员在键盘上敲下W这个字母后，它首先被插线板替换成了另外一个字母（也有可能没替换），我们把这个结果记为v1，接着v1进入了三个转子又被替换成了 v2，最后v2重新进入插线板被替换成了字母E。在这里我们并不知道v1和v2究竟是什么字母，不过这并不影响我们对以上工作原理的理解。

在W-E-R-W这个字母链中，我们想象有三台恩格玛机被插入到这三个字母之间并形成一个循环：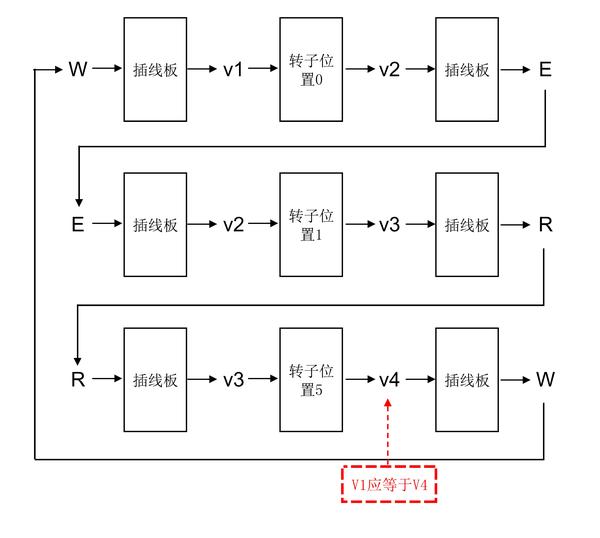

上面这个循环完整的表示了字母W被加密成E，E被加密成R，R又被加密成W这一过程。其中v1,v2,v3,v4都涉及到插线板的替换，由于我们现在还不知道插线板的设置，所以也无法知道这四个字母是什么。不过，由于插线板的设置在整个加密过程中是不变的，所以既然W通过插线板被替换v1，而v4通过插线板被替换成W，我们从而可以肯定v1=v4。这个结论在图中用红色方框标出。另外，在这个循环过程中，v2先是通过插线板被替换成了E，紧接着又在进入第二台恩格玛机后被插线板替换回了v2。我们可以干脆省略掉这一步，让v2直接进入第二台恩格玛机的转子。对于v3也我们也可以做类似的省略，所以上图可以被简化为：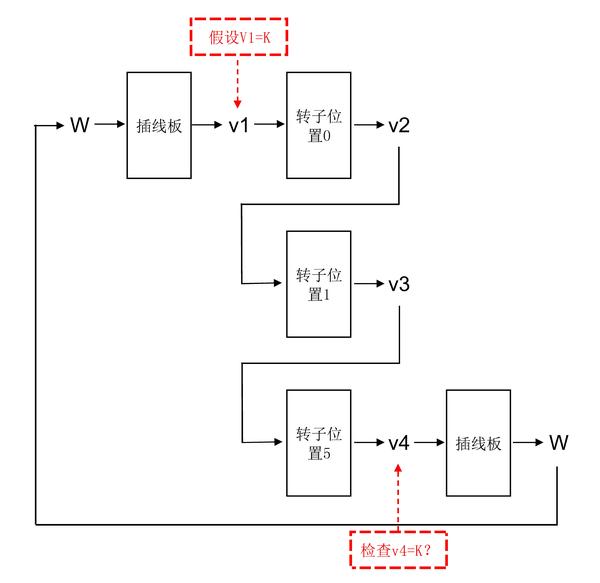

图灵现在只要输入v1（图中假设v1=K），然后试着让这个v1先后通过三台恩格玛机的转子部分得到一个输出结果v4，并对这个结果进行检查。如果v1不等于v4，那么说明目前的恩格玛机转子设置是错误的。如果v1=v4，那么当前的恩格玛机设置有可能是正确的。

虽然图中出现了三台恩格玛机，但由于它们之间的转子位置差距已经确定，所以总的组合数只有60X26X26X26=1054560种。我们再一次看到，只要绕开插线板的干扰，所要检查的转子组合总数立即就下降到了一个可以接受的范围。图灵只要针对这约一百万中组合进行暴力破解，就可以找到所有可能的转子设置组合。如果Crib能够提供足够多的字母链，甚至可以直接锁定唯一可能的转子设置。

什么？你说图灵不知道v1是什么字母？无非只有26种可能性而已，图灵只要在这个地方插上26根电线同时对26个字母进行测试就可以了。

图灵所设计的机器“炸弹”（bombe）就是利用上面的原理对恩格玛密码系统进行了暴力破解。下面我们来看一下炸弹长什么样子，直接上维基百科图：

大家在上面的图中可以看到很多三个一组的转盘，这里面每一个转盘都相当于恩格玛机中的一个转子，所以每组转盘就相当于一台恩格玛机。一台标准的“炸弹”一共有36组这样的转盘。

英国人把准备好的Crib输入“炸弹”后，机器就会根据输入的内容进行暴力破解，如果遇到可能的解，它就会停止下来供工作人员停下来记录结果。而当它没有停下来的时候，人类所能做的就只有站在旁边等待——因为机器创造出来的密码怪兽，只有机器才能战胜。

以上。

PS：评论区里有人留言说答主没有解释原问题中关于德军女友名字Cally对于英军有什么用。我没有看这部电影，但是猜测这里指的应该是很多德军发报员在被要求随机选择三个字母作为信息密钥的时候，为了省事就在键盘上上随便敲下ABC或者XYZ这样简单的组合，也有人为了方便记忆就干脆直接自己女友名字的前三个字母。

出现这样的现象并不是恩格玛机本身的问题，而是人性的弱点造成的。英军在发现这一现象后，就针对以上这些常见的组合进行优先破解，从而缩短获取密钥的时间。