New to Machine Learning? Avoid these three mistakes

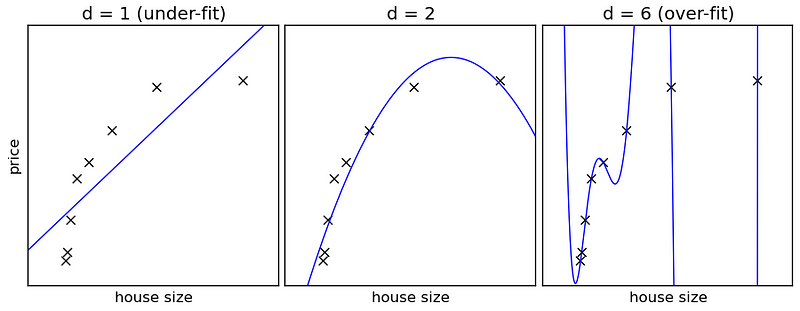
Machine learning is a field ofcomputer science where algorithms(算法) improve their performance at a certain task as more data are observed.To do so,algorithms(算法) select ahypothesis(假设) that best explains the data at hand with the hope that the hypothesis wouldgeneralize to future (unseen) data. Take the left panel(仪表板) in the figure in the header, the crossesdenote(表示) the observed data projected in atwo-dimensional(二维的) space?—?in this case house prices and their corresponding size in square meters. The blue line is the algorithm’s best hypothesis to explain the observed data. It states “there is a linear(线的) relationship between the price and size of a house. As the house’s size increases, so does its price in linearincrements(增量).” Now using this hypothesis, I canpredict(预报) the price of an unseen datapoint based on its size. As thedimensions(规模) of the data increase, the hypotheses that explain the data become morecomplex(复杂的).However, given that we are using afinite(有限的)sample(样品) ofobservations(观察) to learn our hypothesis, finding anadequate(充足的) hypothesis thatgeneralizes(概括) to unseen data isnontrivial(非平凡的). There are three majorpitfalls(陷阱) one can fall into that will prevent you from having ageneralizable(可归纳的) model andhence(因此) the conclusions of your hypothesis will be in doubt.

Occam’s Razor奥卡姆剃刀

Occam’s razor is a principle(原理) attributed(归属) toWilliam of Occama 14th centuryphilosopher(哲学家). Occam’s razoradvocates(提倡者) for choosing the simplest hypothesis that explains your data, yet no simpler. While thisnotion(概念) is simple andelegant(高雅的),it is often misunderstood to mean that we must select the simplest hypothesis possibleregardless(不管) of performance.

The simplest hypothesis that fits the data is also the mostplausible(貌似可信的)

In their 2008 paper in Nature, Johan Nyberg and colleagues used a4-levelartificial(人造的)neural(神经的) network to predictseasonal(季节的) hurricane counts using two or threeenvironmental(环境的)variables(变量). The authors reportedstellar(星的)accuracy(精确度) in predicting seasonal North Atlantic hurricane counts, however their modelviolates(违反) Occam’s razor and most certainly doesn’t generalize to unseen data. The razor was violated when the hypothesis or model selected to describe the relationship between environmental data and seasonal hurricane counts wasgenerated(形成) using a four-layer neural network. A four-layer neural network can modelvirtually(事实上) any function no matter how complex and could fit a small dataset very well but fail to generalize to unseen data. The rightmost panel in the top figure shows such incident. The hypothesis selected by the algorithm (the bluecurve(曲线)) to explain the data is so complex that it fits through every single data point. That is: for any given house size in the training data, I can give you withpinpoint(精确的) accuracy the price it would sell for. It doesn’t take much to observe that even a human couldn’t be thataccurate(精确的). We could give you a very closeestimate(估计) of the price, but to predict the selling price of a house, within a few dollars , every single time is impossible.

Think of overfitting(过适) asmemorizing(记忆) as opposed to learning.

The pitfall of selecting too complex a hypothesis is known asoverfitting. Think of overfitting as memorizing as opposed to learning. If you are a child and you are memorizing how to add numbers you may memorize the sums of any pair of integers(整数) between 0 and 10. However, when asked tocalculate(计算) 11 + 12 you will be unable to because you have never seen 11 or 12, and therefore couldn’t memorize their sum. That’s what happens to an overfitted model, it gets too lazy to learn the general principle that explains the data and instead memorizes the data.

Data leakage数据泄漏

Data leakage occurs when the data you are using to learn a hypothesis(假设) happens to have the information you are trying topredict(预报). The most basic form of dataleakage(泄漏) would be to use the same data that we want to predict asinput(投入) to our model (e.g. use the price of a house to predict the price of the same house). However, most often data leakage occurssubtly(精细地) andinadvertently(非故意地). For example, one may wish to learn foranomalies(异常) as opposed to raw data, that is adeviations(偏差) from a long-term mean. However, many fail to remove the test databefore computing the anomalies andhence(因此) the anomalies carry some information about the data you want to predict since they influenced the mean and standard deviation before being removed.

The are several ways to avoid data leakage asoutlined(概述) byClaudia Perlich in her great paper on the subject. However, there is no silver bullet(子弹)?—?sometimes you mayinherit(继承) acorrupt(腐败的) dataset without even realizing it. One way to spot data leakage is if you are doing very poorly on unseen independent data. For example, say you got a dataset from someone thatspanned(生活期有限的) 2000-2010, but you started collecting you own data from 2011 onward. If your model’s performance is poor on the newly collected data it may be a sign of data leakage. You must resist the urge(强烈的欲望) toretrain(重新教育) the model with both thepotentially(可能地) corrupt and new data.Instated(任命), either try toidentify(确定) the causes of poor performance on the new data or, better yet, independentlyreconstruct(重建) the entire dataset. As a rule ofthumb(拇指), your best defense is to always bemindful(留心的) of the possibility of data leakage in any dataset.

For every Apple that became a success there were 1000 other startups that died trying.

Sampling Bias抽样偏差

Sampling bias is the case when youshortchange(欺骗) your model by training it on abiased(有偏见的) or non-random dataset, which results in a poorlygeneralizable(可归纳的) hypothesis. In the case of housing prices,sampling(取样) bias occurs if, for some reason, all the house prices/sizes you collected were of hugemansions(大厦). However, when it was time to test your model and the first price you needed to predict was that of a 2-bedroom apartment you couldn’t predict it. Sampling bias happens very frequently mainly because, as humans,we arenotorious(声名狼藉的) for being biased (nonrandom(非随机的)) samplers. One of the most common examples of this bias happens in startups andinvesting(投资). If you attend any business school course, they will use all these “case studies” of how to build a successful company. Such case studies actuallydepict(描述) the anomalies and not thenorm(规范) as most companies fail?—?For every Apple that became a success there were 1000 other startups that died trying. So to build anautomated(自动化) data-driveninvestment(投资)strategy(战略) you would need samples from both successful and unsuccessful companies.

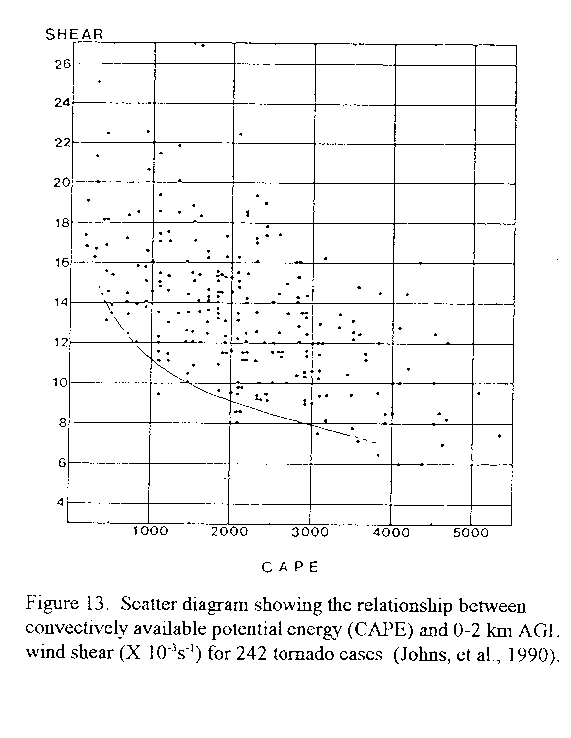
The figure above (Figure 13) is a concrete(混凝土的) example of sampling bias. Say you want to predict whether a tornado is going to originate at certain location based on two environmental conditions:wind shear and convective(对流的) available potential energy (CAPE). We don’t have to worry about what thesevariables(变量) actually mean, but Figure 13 shows the windshear(切变) and CAPEassociated(交往) with 242tornado(龙卷风) cases. We can fit a model to these data but it will certainly notgeneralize(概括) because we failed to include shear and CAPE values when tornadosdid not occur. In order for our model to separate betweenpositive(积极的) (tornados) andnegative(负的) (no tornados) events we must train it using both populations.

There you have it. Being mindful(留心的) of theselimitations(限制) does notguarantee(保证) that your MLalgorithm(算法) will solve all your problems, but it certainly reduces therisk(风险) of being disappointed when your model doesn’t generalize to unseen data. Now go on young Jedi: train your model, you must!