【数据结构】——排序算法——1.3、二叉树排序

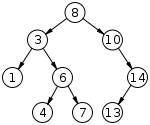
二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树（英语：ordered binary tree），排序二叉树（英语：sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点（英语：no duplicate nodes）。二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等。

在二叉查找树b中查找x的过程为：

1. 若b是空树，则搜索失败，否则：
2. 若x等于b的根节点的数据域之值，则查找成功；否则：
3. 若x小于b的根节点的数据域之值，则搜索左子树；否则：
4. 查找右子树。

public class OrderTree {
    public static void main(String[] args) {
        /**
         *                        ***4***
         *                        *2***6*
         *                        1*3*5*7
         * 
         */
        int[] a = {4,2,1,3,6,5,7,8,9};
        BTree root = new BTree();
        createOrder(a, root);
        System.out.println("\npre order:");
        preOrder(root);
        System.out.println("\nmid order:");
        midOrder(root);
        System.out.println("\nlast order:");
        lastOrder(root);
        List<Point> points = new ArrayList<Point>();
        // 将tree的节点转化为坐标
        int floors = totalfloor(root);
        System.out.println("\nfloors:"+floors);
        printTree(root, points, 0, -1,floors);
         
        // 按照  row,col 对 坐标进行排序方便打印
        Collections.sort(points);
        // 按每点 5个字符宽进行打印（需要进行坐标系转换）， 当data==-1时 显示 *
        int row = 0;
        StringBuilder sb = new StringBuilder();
        int totalLength = 1*(squat(2, floors)-1);
        for(Point p : points){
            if(row == p.row){
                sb.append(printTimes("*",1*p.col-sb.length()));
                sb.append(printWidth(""+p.data, 1));
            }else{
                if(sb.length()< totalLength){
                    sb.append(printTimes("*", totalLength-sb.length()));
                }
                System.out.println(sb.toString());
                sb = new StringBuilder();
                row++;
                sb.append(printTimes("*",1*p.col-sb.length()));
                sb.append(printWidth(""+p.data, 1));
            }
        }
        if(sb.length()< totalLength){
            sb.append(printTimes("*", totalLength-sb.length()));
        }
        System.out.println(sb.toString());
         
         
    }
    static int totalfloor(BTree root){
        if(root == null)return 0;
        return internalLoop(root, 0);
    }
    static int internalLoop(BTree root,int floor){
        if(root != null){
            floor++;
            int left = internalLoop(root.left, floor);
            int right = internalLoop(root.right, floor);
            return Math.max(left, right);
        }
             
        else return floor;
    }
    static String printTimes(String s,int time){
        StringBuilder sb = new StringBuilder();
        for(int i=0;i<time;i++){
            sb.append(s);
        }
        return sb.toString();
    }
    static String printWidth(String s ,int width){
        if(s == null ){
            return printTimes(" ", width);
        }else{
            if(s.length() < width){
                return new StringBuilder(s).append(printTimes("*", width-s.length())).toString();
            }else{
                return s.substring(0,width);
            }
        }
    }
    static class Point implements Comparable<Point>{
        public Point(int row,int col,int data){
            this.row = row;
            this.col = col;
            this.data = data;
        }
        int row = 0;
        int col = 0;
        int data = -1;
        @Override
        public int compareTo(Point o) {
            if(this.row == o.row){
                if(col == o.col)
                    return 0;
                else if(col < o.col){
                    return -1;
                }else{
                    return 1;
                }
            }else if(row < o.row){
                return -1;
            }else{
                return 1;
            }
        }
         
    }
    static void printTree(BTree root,List<Point> points,int row,int col,int floors){
        if(root != null){
            int inter = squat(2, floors-1)-1;
            if(col == -1){
                col = inter;
            }
            /**
             *                           ***0***
             *                           *0***0*
             *                           0*0*0*0
             * 
             */
            points.add(new Point(row, col, root.data));
            printTree(root.left,points,row+1, col - ((inter-1)/2)-1,floors -1);
            printTree(root.right,points,row+1,col + (inter-1)/2+1 ,floors -1);
        }
    }
    static int squat(int s,int b){
        if(b == 0) return 1;
        int result = 1;
        for(int i=0;i<b ;i++){
            result *=s;
        }
        return result;
    }
    static void preOrder(BTree root){
        if(root == null) {
            return ;
        }
        System.out.print("-"+root.data);
        preOrder(root.left);
        preOrder(root.right);
    }
    static void midOrder(BTree root){
        if(root == null) return ;
        midOrder(root.left);
        System.out.print("-"+root.data);
        midOrder(root.right);
    }
    static void lastOrder(BTree root){
        if(root == null) return ;
        lastOrder(root.left);
        lastOrder(root.right);
        System.out.print("-"+root.data);
    }
     
     
    // 左边小，右边大，相等时放左边
    static void createOrder(int[] a,BTree root){
         
        if(a == null || a.length == 0) return ;
        for(int i=0;i<a.length;i++){
            if(i==0){
                root.data = a[i];
            }else{
                BTree leaf = new BTree();
                leaf.data = a[i];
                insert(root,leaf);
            }
        }
    }
    static void insert(BTree root,BTree leaf){
        if(root.data == leaf.data){ // == 放左边
            if(root.left == null){
                root.left = leaf;
            }else{
                insert(root.left,leaf);
            }
        }else if(root.data > leaf.data){ // > 放左边
            if(root.left == null){
                root.left = leaf;
            }else{
                insert(root.left,leaf);
            }
        }else{                          // < 放右边
            if(root.right == null){
                root.right = leaf;
            }else{
                insert(root.right,leaf);
            }
        }
    }
     
    static class BTree{
        BTree left;
        BTree right;
        int data;
    }
}