Dijkstra算法

浏览数：18 / 时间：2015年06月08日

http://ghj19850926.blog.163.com/blog/static/1859156020141115522903/

Dijkstra算法又称为单源最短路径，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最短路径问题。
      设G=（V，E）是一个有向图，V表示顶点，E表示边。它的每一条边（i，j）属于E，都有一个非负权W（I,j），在G中指定一个结点v0，要求把从v0到G的每一个接vj（vj属于V）的最短有向路径找出来（或者指出不存在）。
      Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离
基本思想是：
      设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。
基本步骤：
1、把所有结点分成两组：
      第一组：包括已经确定最短路径的结点；
      第二组：包括尚未确定最短路径的结点。
2、开始时，第一组只包含起点，第二组包含剩余的点；
3、用贪心的策略，按最短路径长度递增的顺序把第二组的结点加到第一组去，直到v0可达的所有结点都包含于第一组中。在这个过程中，不断更新最短路径，总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。
4、每个结点对应一个距离值，第一组结点对应的距离就是v0到此结点的最短路径长度，第二组结点对应的距离值就是v0由第一组结点到此结点的最短路径长度。
5、直到所有的顶点都扫描完毕（v0可达的所有结点都包含于第一组中），找到v0到其它各点的所有最短路径。

动画演示：http://www.jcc.jx.cn/kejiandb/Dijkstra.swf

如图：求0点到其他点的最短路径。

技术分享

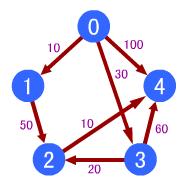
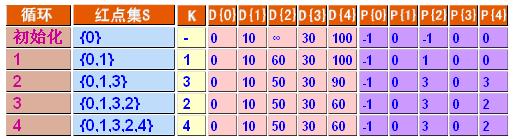
(1)开始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中，最短路径为v1，因此s1={v0,v1},由于v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中，最短路径为v3，因此s1={v0,v1,v3},由于v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；
(4)在还未进入s1的顶点之中，最短路径为v2，因此s1={v0,v1,v3,v2},由于v2到v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,60};
数据结构：
(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离，10000表示无通路：
(2)用数组dist[i..j]表示最短路径；
(3)用集合s表示找到最短路径的结点。

//单源最短路（dijkstra算法）
2 技术分享

program dijkstra;
3 技术分享

const max=10000; //表示无通路
4 技术分享

type jihe=set of 0..100; //顶点数
5 技术分享

var
6

a:array[0..100,0..100] of integer;//各点之间的距离
7 技术分享

dist:array[0..100] of integer; //最短路径
8 技术分享

i,j,k,m,n:integer;
9 技术分享

s:jihe;
10 技术分享

procedure init;
12 技术分享

begin
13

s:=[0]; //开始集合只包含源点
14 技术分享

readln(n);
15 技术分享

assign(input,‘dijs.in‘);reset(input);
16 技术分享

for i:=0 to n do //读入各点之间的距离
17 技术分享

for j:=0 to n do
18 技术分享

read(a[i,j]);
19 技术分享

for i:=0 to n do //源点到各点之间的直接距离
20 技术分享

dist[i]:=a[0,i];
21 技术分享

end;
22

procedure dijsk;
24 技术分享

begin
25

for i:=0 to n do
26 技术分享

begin
27

m:=0;
28

dist[m]:=max; //初始化源点到各点的最小距离为无穷
29 技术分享

for j:=1 to n do
30 技术分享

if(not(j in s))and(dist[m]>dist[j]) then //找出当前的最小距离
31 技术分享

m:=j; //记录找到的顶点
32 技术分享

s:=s+[m]; //把顶点加入集合
33 技术分享

for k:=0 to n do //更新经过新节点到其它点之间的最小距离
34 技术分享

if(not(k in s))and(dist[k]>dist[m]+a[m,k]) then
35 技术分享

dist[k]:=dist[m]+a[m,k];
36 技术分享

end;
37

end;
38

begin
40

init;
41

dijsk;
42

for i:=1 to n do
43 技术分享

writeln(i,‘:‘,dist[i]);
44 技术分享

close(input);
45 技术分享

end.

转：http://www.cnblogs.com/gzydn/archive/2009/07/09/1520019.html

http://ghj19850926.blog.163.com/blog/static/185915602014112351326191/

Dijkstra算法解决了有向图上带正权值的单源最短路径问题，其运行时间要比Bellman-Ford算法低，但适用范围比Bellman-Ford算法窄。

迪杰斯特拉提出的按路径长度递增次序来产生源点到各顶点的最短路径的算法思想是：对有n个顶点的有向连通网络G=(V, E)，首先从V中取出源点u0放入最短路径顶点集合U中，这时的最短路径网络S=({u0}, {?}); 然后从u?U和v?V－U中找一条代价最小的边(u*, v*)加入到S中去，此时S=({u0, v*}, {(u0, v*)})。每往U中增加一个顶点，则要对V－U中的各顶点的权值进行一次修正。若加进v*作为中间顶点，使得从u0到其他属于V－U的顶点vi的路径不加v*时最短，则修改u0到vi的权值，即以(u0, v*)的权值加上(v*, vi )的权值来代替原(u0, vi )的权值，否则不修改u0到vi的权值。接着再从权值修正后的V－U中选择最短的边加入S中，如此反复，直到U=V为止。

上面的说明都很抽象，下面图解算法思想：

原始图为：

技术分享

寻找最短路径的过程如下：

技术分享

对第一个图中的有向网络按以上算法思想处理，所求得的从源点F到其余顶点的最短路径的过程如图13.16所示。其中单圆圈表示U中的顶点，而双圆圈表示V－U中的顶点。连接U中两个顶点的有向边用实线表示，连接U和V－U中两个顶点的有向边用虚线表示。圆圈旁的数字为源点到该顶点当前的距离值。
初始时，S中只有一个源点F，它到V－U中各顶点的路径如图13.16(a)所示；选择图13.16(a)中最小代价边(F, B)，同时由于路径(F, A)大于(F, B, A)和(F, C)大于(F, B, C)，进行相应调整可得到图13.16(b)；选择图13.16(b)中的最小代价边(B, C)，同时由于(F, B, A)大于(F, B, C, A)，进行相应调整可得到图13.16(c)；选择图13.16(c)中最小代价边(C, A)即可得到图13.16(d)；选择图13.16(d)中最小代价边(F, D) 即可得到图13.16(e); 最后选择(F, E)即可得到图13.16( f )。

具体的程序实现如下：

[cpp] view plain copy