排列算法 C++实现
1.什么是排列？
排列的任务是确定
个不同的元素的排序的可能性。从下边的示意图可看出，3个不同颜色的彩球一共有6种不同的排列方式，因此有如下定理：“个不同的元素可以有
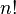种不同的排列方式，即的阶乘。”因此上面的例子的算法是3 !
= 6。
为什么是3的阶乘呢？因为第一个位置有3种颜色可选，除去第一个位置，第二个位置就只有2种颜色可选了，确定好第一位置和第二个位置，第三个位置自动就确定下来了，故一共有3*2*1种可能就是3的阶乘，6种可能。
2.计算机中的C++实现
这个其实是一个蛮难的问题，最普遍的是用递归实现，不过递归效率比较低。
// Perm.cpp : Defines the entry point for the console application.
//
#include "stdafx.h"
#include <iostream>
using namespace std;
template <class T>
inline void Swap(T& a, T& b)
{// 交换a和b
T temp = a; a = b; b = temp;
}
template<class T>
void Perm(T list[], int k, int m)
{ //生成list [k：m ]的所有排列方式
int i;
if (k == m) {//输出一个排列方式
for (i = 0; i <= m; i++)
cout << list [i];
cout << endl;
}
else // 每次交换产生一个新排列
for (i=k; i <= m; i++) {
Swap (list[k], list[i]);
Perm (list, k+1, m);
Swap (list[k], list[i]);
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int a[3] = {1, 2, 3};
Perm(a,0,2);
system("pause");
return 0;
}
结果如下：
老实说，这样写是能出结果，但是可能是我脑子不好使，竟然看不懂，递归的代码特别不容易看懂。后面很努力地看了下，解释如下：
数学中我们知道求1，2，3的排列，第一个位置有3中可能，即1，2，或者3。给人的感觉是物理的感觉，从1，2，3中，每次取一个。这样在计算机中很难表达，在计算机中，有个简便的处理手段，就是交换，跟自己包括后面所有的数交换一次就行了，即得到
1，2，3； // 1 跟 1交换
2，1，3； // 1 跟 2 交换 (又是从1，2，3开始，所以每次交换完都要交换回去，复原)
3，2，1 ；// 1 跟 3 交换
(又是从1，2，3开始，所以每次交换完都要交换回去，复原)
上面的代码又有这样的意思：总共的可能又变成 1 + (2, 3)的排列，2 + (1, 3)的排列， 3 + (2, 1)的排列。 那如何求 2，3的排列呢？ 又是交换，2跟2交换，2跟3交换。 1，3 和 2，1是同样道理。
这样一共是3 * 2 共 6 种可能。
郑重声明：本站内容如果来自互联网及其他传播媒体，其版权均属原媒体及文章作者所有。转载目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。
