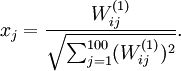deep learning 自编码算法详细理解与代码实现（超详细）
在有监督学习中，训练样本是有类别标签的。现在假设我们只有一个没有带类别标签的训练样本集合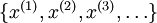 
，其中 
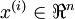。自编码神经网络是一种无监督学习算法，它使用了反向传播算法，并让目标值等于输入值，比如 
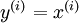。下图是一个自编码神经网络的示例。通过训练，我们使输出 
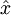接近于输入 
。当我们为自编码神经网络加入某些限制，比如限定隐藏神经元的数量，我们就可以从输入数据中发现一些有趣的结构。举例来说，假设某个自编码神经网络的输入 是一张 张8*8 图像（共64个像素）的像素灰度值，于是 n=64，其隐藏层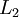 
中有25个隐藏神经元。注意，输出也是64维的 
。由于只有25个隐藏神经元，我们迫使自编码神经网络去学习输入数据的压缩表示，也就是说，它必须从25维的隐藏神经元激活度向量 
中重构出64维的像素灰度值输入 。如果网络的输入数据是完全随机的，比如每一个输入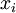 
都是一个跟其它特征完全无关的独立同分布高斯随机变量，那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构，比如某些输入特征是彼此相关的，那么这一算法就可以发现输入数据中的这些相关性。网络训练好以后，每一个输入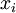对应的LayerL2 
就相当于降维后的数据。(跟pca理解差不多，只是pca 是线性降维，这里因为有sigmoid非线性激活函数的原因，所以这里应该可看做是非线性的降维。）
现在我们实验一下：我们有十张64*64的图片,十张图片如下：
我们从这十张图片中随机取出10000个小碎片，小碎片是8*8的小图片（叫做patch，或者掩模），这10000个patch就是10000个样本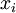，我们很容易理解这10000个样本之间肯定有联系。那么接下来我们就实现这个自编码算法。
我们先得到这10000个样本（注意样本都约束在了[0.1,0.9]之间，如果不约束，得到的是平凡解，但这里说输入的约束是
）。
得到样本的程序如下：
1: function patches = sampleIMAGES() 2: % sampleIMAGES3: % Returns 10000 patches for training
4: load IMAGES; % load images from disk IMAGES是一个512*512*10的数组。 5: patchsize = 8; % we‘ll use 8x8 patches 6: numpatches = 10000; 7: patches = zeros(patchsize*patchsize, numpatches);%这个patches是一个矩阵 8: %每一列是一个64的列向量，是把每一个8*8的掩模变成这样一个向量，然后这个矩阵有 9: %10000个列。也就是说从10幅512*512的图像中弄出来10000个掩模。现在初始化它。 10: %% 从10幅512*512的图像中随机选出10000个8*8的掩模，然后制作 patches 11: image_size=size(IMAGES); 12: i=randi(image_size(1)-patchsize+1,1,numpatches); 13: %在开区间（0，image_size(1)-patchsize+1）之间生成一个1行10000列的向量 14: %也就是在一副512*512的图像中的行号中（不包括最后的7行，因为选了也构不成8*8的掩模了） 15: %随意选出10000个数字组成向量A。下面这行是在列号中选10000个元素的向量B， 16: %这样每一次从A和B中选出一个数a，b，然后a+7，b+7，这样a，b，a+7，b+7就组成了一个 17: %8*8的掩模。（注意是选择哪个地方的掩模之前，要先从十幅图像中选一幅图像) 18: %然后依次这么做，就得到了10000个掩模，然后把每个掩模弄成8*8的向量， 19: %依次排到 patches的每一列上就得到了 patches。 20: j=randi(image_size(2)-patchsize+1,1,numpatches); 21: k=randi(image_size(3),1,numpatches);22: for num=1:numpatches
23: patches(:,num)=reshape(IMAGES(i(num):i(num)+patchsize-1,j(num):j(num)+patchsize-1,k(num)),1,patchsize*patchsize); 24: end 25: %% --------------------------------------------------------------- 26: % For the autoencoder to work well we need to normalize the data27: % Specifically, since the output of the network is bounded between [0,1]
28: % (due to the sigmoid activation function), we have to make sure 29: % the range of pixel values is also bounded between [0,1]
30: patches = normalizeData(patches); 31: display_network(patches(:,randi(size(patches,2),200,1)),8);%这个是随机从那10000个patch里面选出来200个patch，看看是不是 32: %弄对了。 33: end %这个end是说明patches这个function结束了，因为下面还有一个function，在一个文件里，所以一个function完了必须写end 34: 35: %% --------------------------------------------------------------- 36: function patches = normalizeData(patches) 37: % Remove DC (mean of images). 38: patches = bsxfun(@minus, patches, mean(patches)); 39: % mean(patches)对patches每一列算出一个平均值。也就是每一组样本算出一个平均值。 40: %mean(patches)是一个1*10000的行向量，这里 patches是一个64*10000的矩阵，按理说 41: %不能相减，但这里 用到了bsxfun（@minus,），那么mean(patches)会自动复制64行， 42: %然后也变成一个64*10000的矩阵，然后相减。 43: 44: % Truncate to +/-3 standard deviations and scale to -1 to 1 45: pstd = 3 * std(patches(:));%patches(:)是把这个矩阵变成一个向量。然后std，也就是 46: %求所有10000个掩模所有像素值的标准差，这里如果你不是很明白为什么要把所以样本一块求标准差， 47: %而不是一个样本组一个样本组的求标准差。并且还最后把所有像素的标准差*3。解释一下，以前求 48: %数据都是一个样本组一个样本组进行归一化，那是把数据进行归一化，也就是均值为0，方差为1，但是 49: %这样并不能保证所有的数据都在[-1,1]之间，只是方差为1。但是我们知道我们把所有数据减去均值 50: %的话，那么所有数据的99.7%都会落在[-3*标准差，3*标准差]之间，所以我们只需要把剩下的0.03%的数据都 51: %置成-3*标准差或3*标准差即可。这样所有数据都在[-3*标准差，3*标准差]之间，然后我们除以 52: %3*标准差，那么素有数据都会在[-1,1]之间了。注意这里是将所有数据一块处理，而不需要一组一组样本处理， 53: %因为这里并不需要处理后的每个样本满足标准正态分布:均值为0，方差为1那种关系，也不可能满足，所以 54: %数据一块处理即可。 55: patches = max(min(patches, pstd), -pstd) / pstd; 56: %min(patches, pstd)意思是patches这个矩阵中元素如果大于pstd，那么这个元素就是prsd。 57: %也就是上限是pstd，然后这里再max，也就是矩阵元素的下限是-petd。 58: 59: % Rescale from [-1,1] to [0.1,0.9] 60: patches = (patches + 1) * 0.4 + 0.1; 61: end随机选出200个样本/pitch（也就是从那10幅图像中随机取出的8*8的小碎片）可以看一下：
接下来要做的就是求出cost function函数，那么这里的cost function是什么那？我们已经从上一节中知道cost function（加了L2正则项）：
那么我们通过梯度下降法就可以得到收敛的参数。那么关键就是求cost function的偏导数。
并且我们知道代价函数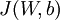 
对每一个参数的偏导数可通过如下公式求：
回答一下为什么要加这种洗属性约束呢？因为这个网络是模拟的人脑，而人脑也是一个神经元分层工作的系统，进来一个图像后，首先第一层的神经元开始工作，因为神经元被激活是需要能量的，所以只有很少的神经元被激活，工作，大部分都处于被抑制状态。
然后，这个稀疏约束项是什么呢？首先对于隐藏层的一个神经元，我们使用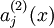 
来表示在给定输入为 情况下，自编码神经网络隐藏神经元 
的激活度，隐藏神经元 的平均活跃度就是：
为了书写方面，我们令
，
加入稀疏惩罚项以后，我们的cost function 就变成了：
最后程序中的opttheta就是我们训练好的神经网络参数。
我们既然训练好了，我们就想好好我们的训练学习好了什么东西、怎么看呢？
我们之前说过，第二层神经元与第一层的关系相当于Pca一样，第二层神经元值的向量以原始的样本向量相当于降维以后的结果。只是pca是线性的，而这里因为有logistic函数，所以是非线性的降维。那么隐藏层那一层的每一个神经元
的值代表的含义是什么呢？我们仍然可以类比pca，如图所示：
我们看到pca是将原来的数据在新坐标系下表示，并且把某些坐标轴去掉（把区分数据不明显的坐标轴去掉），而使数据降维的过程。所以降维后样本每一维的数据可以看成：在新的基下或新的特征下，样本在这个特征表达多少或程度多少。
所以类别一下：隐藏层那一层的每一个神经元
的值代表的就是在新选择的某一个特征下（因为隐藏层有25个神经元，所以新选了25个特征，然后将样本用这25个特征表示出来（应该不是线性叠加），新的数据就有25维，每一维的数值就是样本在这个特征的表达式多少。），原样本数据在这个样本表达了多少。那么我们应该如何找到这个新特征是什么呢？肯定不是
的值，因为它是样本在某个特征下的表达程度，因为样本可以用这25个特非线性性叠加起来。所以这些特征应该和原样本pitch大小相同，类似于特征量一样。那么应该怎么求呢？ 做法是对下面这个方程求最大值。
因为参数是已知的，如果我们求隐藏层某一个神经元的激活值求最大值，那么就可以找到使这个神经元激活的输入是多少，那么这个输入就是其中的一个特征。一般来说使其中的一个神经元激活，另外其他的就不一定激活了，因为我们已经加入了激活值的稀疏项。还有一个问题需要注意：如果你的样本xi的值都很大的话，
得到平凡解，所以必须给加约束，若假设输入有范数约束
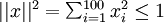，则令隐藏单元
得到最大激励的输入应由下面公式计算的像素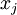
给出（共需计算100个像素，j=1,…,100）：
当我们用上式算出各像素的值、把它们组成一幅图像、并将图像呈现在我们面前之时，那么这个特征我们就可以看到了。并且我们看到的这个图像是带有有界范数的图像。注意我们这是为了向可视化特征才给输入x加了范数约束，因为不加约束会得到平凡解，但是一般的情况你的输入样本是不需要约束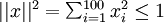这种的约束。不过样本应该也要进行归一化，把数据归一到[0,1]之间。
可视化特征的程序为：
W1 = reshape(opttheta(1:hiddenSize*visibleSize), hiddenSize, visibleSize);
display_network(W1‘, 12); %display_network函数中已经包括对输入加了范数约束。
那么25个特征如图所示：
我们可以看出来这25个特征都是一些“边缘”特征，为什么会是边缘特征呢？
因为人的神经系统也是分层的，第一层的神经层也是对一幅图像的边缘特征处于激活。详细并且很经典的讲解特征的是这一篇博客，可以参考这里。
参考：http://deeplearning.stanford.edu/wiki/index.php
http://www.cnblogs.com/hrlnw/archive/2013/06/08/3127162.html
http://deeplearning.stanford.edu/wiki/index.php/Exercise:Sparse_Autoencoder
郑重声明：本站内容如果来自互联网及其他传播媒体，其版权均属原媒体及文章作者所有。转载目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。
