探索推荐引擎内部的秘密，第 3 部分: 深入推荐引擎相关算法 - 聚类（四）

浏览数：19 / 时间：2015年06月08日

狄利克雷聚类算法

前面介绍的三种聚类算法都是基于划分的，下面我们简要介绍一个基于概率分布模型的聚类算法，狄利克雷聚类（Dirichlet Processes Clustering）。

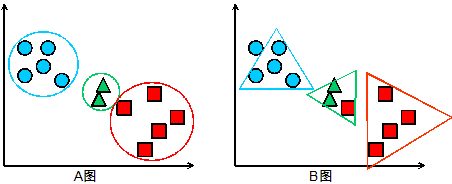
首先我们先简要介绍一下基于概率分布模型的聚类算法（后面简称基于模型的聚类算法）的原理：首先需要定义一个分布模型，简单的例如：圆形，三角形等，复杂的例如正则分布，泊松分布等；然后按照模型对数据进行分类，将不同的对象加入一个模型，模型会增长或者收缩；每一轮过后需要对模型的各个参数进行重新计算，同时估计对象属于这个模型的概率。所以说，基于模型的聚类算法的核心是定义模型，对于一个聚类问题，模型定义的优劣直接影响了聚类的结果，下面给出一个简单的例子，假设我们的问题是将一些二维的点分成三组，在图中用不同的颜色表示，图 A 是采用圆形模型的聚类结果，图 B 是采用三角形模型的聚类结果。可以看出，圆形模型是一个正确的选择，而三角形模型的结果既有遗漏又有误判，是一个错误的选择。

图 3 采用不同模型的聚类结果

Mahout 实现的狄利克雷聚类算法是按照如下过程工作的：首先，我们有一组待聚类的对象和一个分布模型。在 Mahout 中使用 ModelDistribution 生成各种模型。初始状态，我们有一个空的模型，然后尝试将对象加入模型中，然后一步一步计算各个对象属于各个模型的概率。下面清单给出了基于内存实现的狄利克雷聚类算法。

清单 6. 狄利克雷聚类算法示例

 public static void DirichletProcessesClusterInMemory() { 
 // 指定狄利克雷算法的 alpha 参数，它是一个过渡参数，使得对象分布在不同模型前后能进行光滑的过渡
	 double alphaValue = 1.0; 
 // 指定聚类模型的个数
	 int numModels = 3; 
 // 指定 thin 和 burn 间隔参数，它们是用于降低聚类过程中的内存使用量的
	 int thinIntervals = 2; 
	 int burnIntervals = 2; 
 // 指定最大迭代次数
	 int maxIter = 3; 
	 List<VectorWritable> pointVectors = 
	 SimpleDataSet.getPoints(SimpleDataSet.points); 
 // 初始阶段生成空分布模型，这里用的是 NormalModelDistribution 
	 ModelDistribution<VectorWritable> model = 
 new NormalModelDistribution(new VectorWritable(new DenseVector(2))); 
 // 执行聚类
	 DirichletClusterer dc = new DirichletClusterer(pointVectors, model, alphaValue, 
 numModels, thinIntervals, burnIntervals); 
	 List<Cluster[]> result = dc.cluster(maxIter); 
 // 打印聚类结果
	 for(Cluster cluster : result.get(result.size() -1)){ 
		 System.out.println("Cluster id: " + cluster.getId() + " center: " + 
 cluster.getCenter().asFormatString()); 
		 System.out.println("       Points: " + cluster.getNumPoints()); 	
	 } 
 } 

执行结果
 Dirichlet Processes Clustering In Memory Result 
 Cluster id: 0 
 center:{"class":"org.apache.mahout.math.DenseVector",
 "vector":"{\"values\":[5.2727272727272725,5.2727272727272725],
 \"size\":2,\"lengthSquared\":-1.0}"} 
       Points: 11 
 Cluster id: 1 
 center:{"class":"org.apache.mahout.math.DenseVector",
 "vector":"{\"values\":[1.0,2.0],\"size\":2,\"lengthSquared\":-1.0}"} 
       Points: 1 
 Cluster id: 2 
 center:{"class":"org.apache.mahout.math.DenseVector",
 "vector":"{\"values\":[9.0,8.0],\"size\":2,\"lengthSquared\":-1.0}"} 
       Points: 0

Mahout 中提供多种概率分布模型的实现，他们都继承 ModelDistribution，如图 4 所示，用户可以根据自己的数据集的特征选择合适的模型，详细的介绍请参考 Mahout 的官方文档。

图 4 Mahout 中的概率分布模型层次结构

Mahout 聚类算法总结

前面详细介绍了 Mahout 提供的四种聚类算法，这里做一个简要的总结，分析各个算法优缺点，其实，除了这四种以外，Mahout 还提供了一些比较复杂的聚类算法，这里就不一一详细介绍了，详细信息请参考 Mahout Wiki 上给出的聚类算法详细介绍。

表 1 Mahout 聚类算法总结

算法	内存实现	Map/Reduce 实现	簇个数是确定的	簇是否允许重叠
K 均值	KMeansClusterer	KMeansDriver	Y	N
Canopy	CanopyClusterer	CanopyDriver	N	N
模糊 K 均值	FuzzyKMeansClusterer	FuzzyKMeansDriver	Y	Y
狄利克雷	DirichletClusterer	DirichletDriver	N	Y

总结

聚类算法被广泛的运用于信息智能处理系统。本文首先简述了聚类概念与聚类算法思想，使得读者整体上了解聚类这一重要的技术。然后从实际构建应用的角度出发，深入的介绍了开源软件 Apache Mahout 中关于聚类的实现框架，包括了其中的数学模型，各种聚类算法以及在不同基础架构上的实现。通过代码示例，读者可以知道针对他的特定的数据问题，怎么样向量化数据，怎么样选择各种不同的聚类算法。

本系列的下一篇将继续深入了解推荐引擎的相关算法 -- 分类。与聚类一样，分类也是一个数据挖掘的经典问题，主要用于提取描述重要数据类的模型，随后我们可以根据这个模型进行预测，推荐就是一种预测的行为。同时聚类和分类往往也是相辅相成的，他们都为在海量数据上进行高效的推荐提供辅助。所以本系列的下一篇文章将详细介绍各类分类算法，它们的原理，优缺点和实用场景，并给出基于 Apache Mahout 的分类算法的高效实现。

最后，感谢大家对本系列的关注和支持。