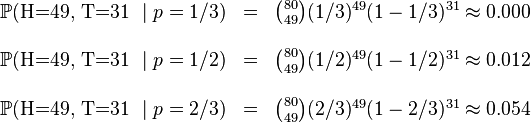【机器学习算法-python实现】最大似然估计(Maximum Likelihood)
1.背景
离散分布,离散有限参数空间[编辑]
考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次(即,我们获取一个采样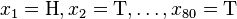 并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为
并把正面的次数记下来,正面记为H,反面记为T)。并把抛出一个正面的概率记为 ,抛出一个反面的概率记为
,抛出一个反面的概率记为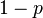 (因此,这里的
(因此,这里的 即相当于上边的
即相当于上边的 )。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为
)。假设我们抛出了49个正面,31个反面,即49次H,31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为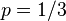 ,
, 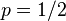 ,
,  .这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
.这些硬币没有标记,所以我们无法知道哪个是哪个。使用最大似然估计,通过这些试验数据(即采样数据),我们可以计算出哪个硬币的可能性最大。这个似然函数取以下三个值中的一个:
我们可以看到当 时,似然函数取得最大值。这就是
时,似然函数取得最大值。这就是 的最大似然估计。
的最大似然估计。
2.实现部分
def Factorial(x):
return reduce(lambda x,y:x*y,range(1,x+1)) ‘‘‘
Created on 2014-8-22
@author: Garvin
Maximum Likelihood theory practic
This code is base on the http://zh.wikipedia.org/wiki/%E6%9C%80%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1
‘‘‘
w=2.0/3
h=49
t=31
def DefineParam():
H=h
T=t
return H,T
def MaximumLikelihood(p=w):
H,T=DefineParam()
f1=Factorial(H+T)/(Factorial(H)*Factorial(T))
f2=(p**H)*((1.0-p)**T)
return f1*f2
def Factorial(x):
return reduce(lambda x,y:x*y,range(1,x+1))

/********************************
* 本文来自博客 “李博Garvin“
* 转载请标明出处:http://blog.csdn.net/buptgshengod
******************************************/
郑重声明:本站内容如果来自互联网及其他传播媒体,其版权均属原媒体及文章作者所有。转载目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,也不构成任何其他建议。