SharePoint Survey WebPart 调查 Web部件

浏览数：23 / 时间：2015年06月09日

Problem Description

Chinachen is a football fanatic, and his favorite football club is Juventus fc. In order to buy a ticket of Juv, he finds a part-time job in Professor Qu’s lab.
And now, Chinachen have received an arduous task——Data Processing.
The data was made up with N positive integer (n1, n2, n3, … ), he may calculate the number

, you can assume

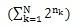mod N =0. Because the number is too big to count, so P mod 1000003 is instead.
Chinachen is puzzled about it, and can’t find a good method to finish the mission, so he asked you to help him.

Input

The first line of input is a T, indicating the test cases number.
There are two lines in each case. The first line of the case is an integer N, and N<=40000. The next line include N integer numbers n1,n2,n3… (ni<=N).

Output

For each test case, print a line containing the test case number ( beginning with 1) followed by the P mod 1000003.

Sample Input

Sample Output

Case 1:4
Case 2:6

又是一条数论题目，最近学习数论，看完书本感觉并不能掌握数论的，还是需要多多练习，多运用才能掌握这个思想武器的。

本题可以简单点过，不需要太高级的数论内容；

但是也可以运用好数论的内容，可以应用上三个数论的内容：

1 扩展欧几里得

2 快速求模

3 乘法逆元(inverse of modulo)

2 快速求模，也可以生成一个数组，因为这里最大是40000，故此数值不大，可以使用数组，然后查表，速度很快。

但是这里使用快速的时间效率也几乎接近常数，没必要保存一个数组。如下面的powMod函数。

3 乘法逆元的应用的原理就是：

如果求a / b % c;

那么可以求得b的乘法逆元e；be % c == 1，那么a / b % c == a / b * b * e % c；相当于 a / b % c == a / b * 1(b*e) % c，这个是求模的性质，相当于一般算术中的一个数乘以其倒数等于1.最后可以化简为a * e % c == a / b % c；

这样做题，可以说非常科学系统，下面速度也算挺快的，而且消耗内存很小。

作者：靖心 http://blog.csdn.net/kenden23/article/details/29363389

#include <cstdio>

class DataProcessing3094
{
	const static int MOD = 1000003;
	long long s, t, g;

	void extGCD(int a, int b)
	{
		if (b == 0)
		{
			s = 1L, t = 0L;
			g = a;
		}
		else
		{
			extGCD(b, a % b);
			long long tmp = s;
			s = t;
			t = tmp - a / b * t;
		}
	}

	long long powMod(long long base, long long num, long long mod)
	{
		long long ans = 1;
		while (num)
		{
			if (num & 1) ans = ans * base % mod;
			base = base * base % mod;
			num >>= 1;
		}
		return ans % mod;
	}
public:
	DataProcessing3094()
	{
		int T, N, a;
		scanf("%d", &T);
		for (int i = 1; i <= T; i++)
		{
			scanf("%d", &N);
			long long ans = 0;
			for (int j = 0; j < N; j++)
			{
				scanf("%d", &a);
				ans = (ans + powMod(2, a, MOD)) % MOD;
			}
			extGCD(MOD, N);//即使g不等于1，最后mod也会约去g			
			t = (t % MOD + MOD) % MOD;//求其最小正整数
			ans = ans * t % MOD;
			printf("Case %d:%I64d\n",i,ans);
		}
	}
};

SharePoint Survey WebPart 调查 Web部件,古老的榕树,5-wow.com

郑重声明：本站内容如果来自互联网及其他传播媒体，其版权均属原媒体及文章作者所有。转载目的在于传递更多信息及用于网络分享，并不代表本站赞同其观点和对其真实性负责，也不构成任何其他建议。

SharePoint Survey WebPart 调查 Web部件