POJ 2007 Scrambled Polygon（计算几何 叉积排序啊）

A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex. 

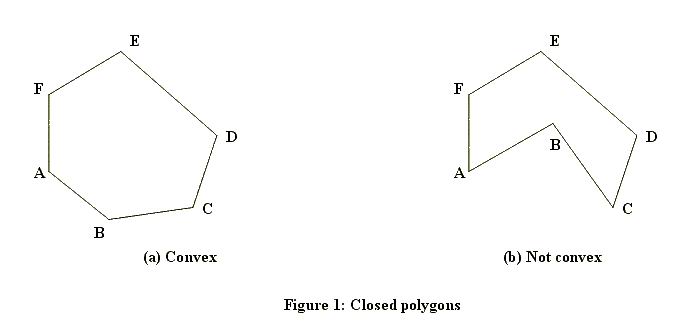
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn‘t have any "dents".) 

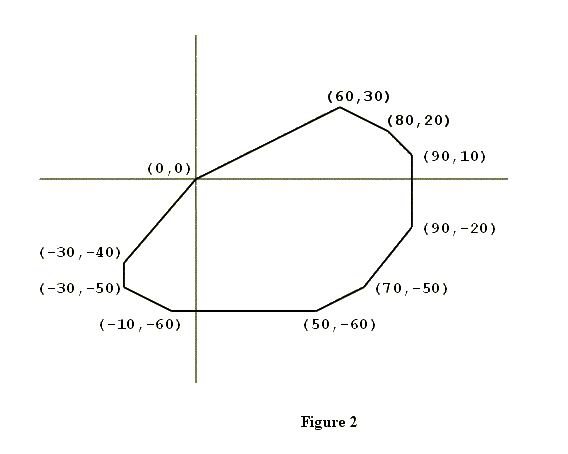
The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem. 

The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0). 

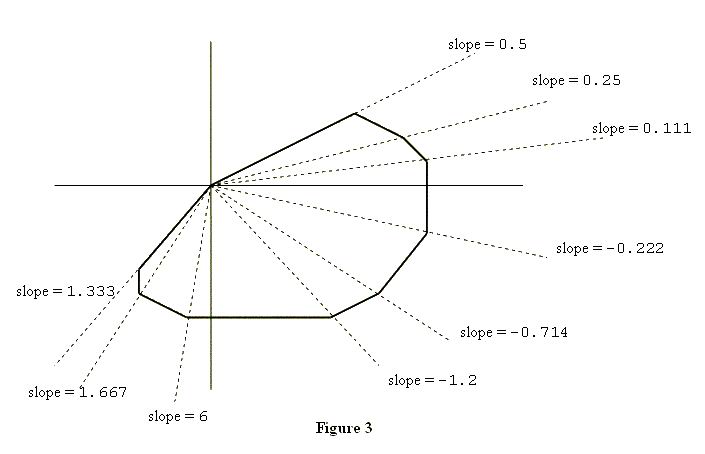
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point. 
 

The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon‘s border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)

Rocky Mountain 2004

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct node
{
    double x, y;
} p[87];
double cross(node p1, node p2, node t1, node t2)
{
    return (p2.x-p1.x)*(t2.y-t1.y)-(t2.x-t1.x)*(p2.y-p1.y);
}
bool cmp(node a, node b)
{
    node tt;
    tt.x = tt.y = 0;
    return cross(tt,a,tt,b)>0;
}
int main()
{
    int i = 0;
    while(~scanf("%lf%lf",&p[i].x,&p[i].y))
    {
        i++;
    }
    sort(p+1,p+i,cmp);
    for(int j = 0; j < i; j++)
    {
        printf("(%.0lf,%.0lf)\n",p[j].x,p[j].y);
    }
    return 0;
}